Рhysics Astronomy Мathematics: Основні теми математики

Числа[ред. • ред. код]

Вивчення кількості починається з чисел, спочатку із знайомих нам натуральних чисел та цілих чисел та арифметичних операцій з ними, які вивчаються варифметиці. Глибші властивості цілих чисел вивчає теорія чисел, до якої належить знаменита Велика теорема Ферма. До невирішених задач теорії чиселналежать припущення щодо простих чисел-близнюків та Гіпотеза Гольдбаха.

У процесі розвитку числової системи, цілі числа виявились підмножиною раціональних чисел (додались дроби). А ці в свою чергу входять до множини дійсних чисел, які використовуються для відображення неперервних величин. Дійсні числа є окремим випадком від комплексних чисел. А вони є першим кроком в ієрархії чисел, яка включає кватерніони та октоніони. Вивчення натуральних чисел призвело до появи трансфінітних чисел, які формалізують поняття нескінченності. Іншою областю дослідження є розмір множини чисел, який призвів до появи кардинальних чисел, а потім до нової концепції нескінченності: чисел алеф, які дають змогу значимо порівняти розмір нескінченно великих множин.

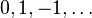$1, 2, \ldots$	$0, 1, -1, \ldots$	$1, -1, \frac{1}{2}, \frac{2}{3}, 0.12,\ldots$
Натуральні числа	Цілі числа	Раціональні числа
$1, -1,\frac{1}{2},0.12,\pi,\sqrt{2},\ldots$	$-1,\frac{1}{2},0.12,\pi,3i+2, e^{i\pi/3},\ldots$	$1,i,j,k, \pi j - \frac{1}{2}k, \dots$
Дійсні числа	Комплексні числа	Кватерніони

Перетворення[ред. • ред. код]

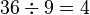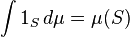$36 \div 9 = 4$			$\int 1_S\,d\mu=\mu(S)$
Арифметика	Диференціальне та інтегральне числення	Векторний аналіз	Математичний аналіз
$\frac{d^2}{dx^2} y = \frac{d}{dx} y + c$
Диференціальні рівняння	Динамічні системи	Теорія хаосу

Арифметика — Векторний аналіз — Математичний аналіз — Теорія міри — Диференціальні рівняння — Динамічні системи — Теорія хаосу — Список функцій

Структури[ред. • ред. код]

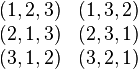$\begin{matrix} (1,2,3) & (1,3,2) \\ (2,1,3) & (2,3,1) \\ (3,1,2) & (3,2,1) \end{matrix}$
Комбінаторика	Теорія чисел	Теорія груп	Теорія графів	Теорія порядку

Абстрактна алгебра — Теорія груп — Алгебраїчні структури — Алгебраїчна геометрія — Теорія чисел — Топологія — Лінійна алгебра — Універсальна алгебра — Теорія категорій — Теорія послідовностей

Просторові відношення[ред. • ред. код]

Дослідження простору спричинило до виникнення геометрії, зокрема Евклідової геометрії. Тригонометрія — це розділ математики, що має справу з відношеннями між сторонами та кутами в трикутнику та з тригонометричними функціями; тут простір виражений в числах, до цього розділу входить знаменита Теорема Піфагора. Сучасні дослідження простору узагальнюють ці ідеї та включають багатовимірну геометрію, неевклідові геометрії (які грають центральну роль в загальній теорії відносності) та топологію. Кількісні та просторові характеристики разом досліджуються в аналітичній геометрії,диференціальній геометрії та алгебричній геометрії. Конвексна геометрія та дискретна геометрія були розроблені, щоб розв'язати задачі в теорії чисел тафункціональному аналізі, але тепер знайшли своє застосування в оптимізації та інформатиці.


Геометрія	Тригонометрія	Диференціальна геометрія	Топологія	Фрактальна геометрія

Геометрія — Тригонометрія — Алгебрична геометрія — Топологія — Диференціальна геометрія — Диференціальна топологія — Алгебрична топологія — Лінійна алгебра — Фрактальна геометрія

Дискретна математика[ред. • ред. код]

Дискретна математика містить засоби, які застосовуються до об'єктів, що можуть приймати лише специфічні, окремі значення (не неперервні).

	$\forall x (P(x) \Rightarrow P(x'))$
Теорія множин	Математична логіка	Теорія обчислюваності	Криптографія	Теорія графів